
Molti radioamatori sanno che, combinando induttanze e capacità in varie configurazioni, possono accordare l’impedenza della loro antenna per farla corrispondere a quella necessaria al loro ricetrasmettitore. Molti, grazie alla loro esperienza, sono anche in grado di valutare grosso modo quanti µH e quanti pF gli serviranno per eseguire accordi sulle varie bande.
Ma qual’è il principio di base che permette ad un accordatore di accordare? Ed è vero che la potenza riflessa dal carico ad alto ROS è dissipata dall’accordatore?
Un esperimento nel mondo reale
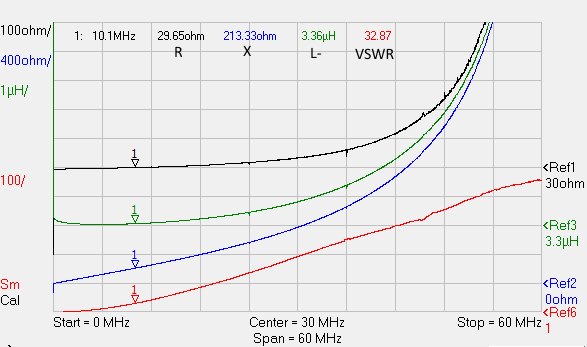
Per avere qualcosa di reale con cui lavorare, ho preparato un carico di test collegando in serie tre resistenze induttive da 8Ω-5W in modo che presentassero sia resistenza che una reattanza rilevante, caso normale quando si tarano le antenne. Ho scelto 10.100MHz come frequenza e ho collegato questo carico di test all’analizzatore vettoriale per vedere che impedenza presentasse:

Il VNA mostra che a 10.100MHz questo carico ha impedenza R=29.65Ω, X=213.33Ω, l’induttanza dei tre resistori è di 3.36µH ed il ROS è piuttosto alto: 32.87.
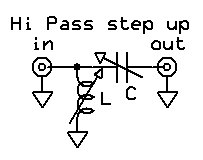
Per eseguire l’accordo, ho scelto un semplice circuito ad “L” passa alto in configurazione “step-up”:
Utilizzando un induttanza “roller” e un condensatore variabile ho creato il mio accordatore ad “L” ed ho accordato il carico a 10.100MHz usando il VNA per misurare il ROS:

Regolando i valori con cura, sono riuscito ad ottenere un accordo pressoché perfetto, con R=49.8Ω, X=0.05Ω e ROS=1.02:
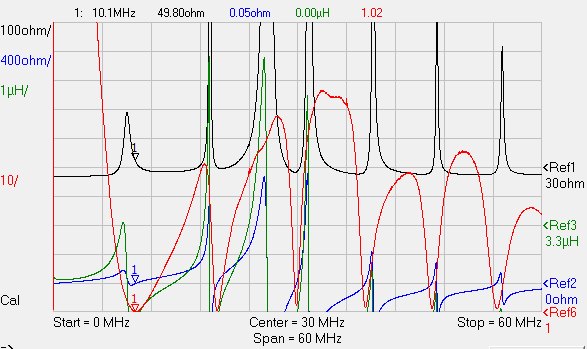
E, fin qui, ci siamo.
Misura dei componenti
Il prossimo passo consiste nel misura l’induttanza del roller e la capacità del condensatore variabile una volta configurati per l’accordo:


Abbiamo che C=66.24pF e L=0.939µH.
Ma perché proprio questi esatti valori riescono ad eseguire l’accordo?
La magia dei circuiti
Il principio che consente ad un accordatore di accordare è quello alla base del “trucco” che anche gli elettrotecnici principianti sfruttano per “creare” nuovi valori di resistenza combinando in serie o parallelo altri resistori a loro disposizione.
Prendiamo due resistori R1 ed R2:

Misuriamo R1=100.048Ω e R2=327.47Ω.
Se li combiniamo in serie, otteniamo [1] Rs=R1+R2=427.518Ω, confermato dalla misura di 427.51Ω.
Se li combiniamo in parallelo, otteniamo invece [2] Rp=1/((1/R1) + (1/R2))=76.635Ω che pure è confermato dalla misura (76.639Ω). L’operazione 1/x è chiamata il reciproco di x, pertanto [2] può essere espressa come il reciproco della somma dei reciproci delle resistenze.
Dalla resistenza all’impedenza
Il caso della resistenza visto sopra è solo un caso speciale, valido per la corrente continua, di un caso più generale chiamato impedenza. L’impedenza descrive un componente in termini di resistenza e di reattanza ad una data frequenza; alla frequenza di 0Hz, otteniamo il caso a corrente continua visto sopra.
Quando misuriamo un’antenna con il nostro analizzatore, possiamo leggere direttamente sul display la resistenza (R) e la reattanza (X) che costituiscono l’impedenza dell’antenna alla frequenza in esame.
È importante sottolineare che l’impedenza è sempre formata da due numeri: R e X. Quando viene indicato un solo numero c’è sempre qualcosa di sottinteso: ad esempio, quando in genere si dice “50Ω” si intende “R=50Ω X=0Ω”.
L’accoppiata di valori R e X che formano l’impedenza descrive un circuito equivalente costituito da un resistore ideale con resistenza R in serie ad un condensatore (se X è negativo), un induttore (se X è positivo). Se X è zero, il circuito corrisponde al solo resistore e si definisce risonante.
Come si calcola la reattanza “X”?
Mentre la componente “R” dell’impedenza è semplicemente la resistenza in Ω, il valore di “X” è leggermente più complicato. Infatti il suo valore, sempre espresso in Ω, dipende dalla frequenza e dalla capacità o induttanza del componente reattivo.
In caso di reattanza induttiva abbiamo: X=2π·f·L
In caso di reattanza capacitiva abbiamo: X=-1 / 2π·f·C
Dove:
- f è la frequenza in MHz
- C è la capacità in µF
- L è l’induttanza in µH
- π è 3.14159
Con queste informazioni possiamo ora calcolare l’impedenza R,X dei componenti dell’accordatori, cioè il condensatore e l’induttore.
L’induttore ha induttanza L=0.939µH; a 10.1MHz la sua reattanza è X=2π·10.1MHz·0.939µH=59.589Ω. Il nostro induttore non è ideale e presenta a 10.1MHz anche una resistenza in serie di circa 1Ω. Pertanto, l’impedenza dell’induttore è:
ZL: 0.939µH@10.1MHz → RL=1Ω, XL=59.589Ω
Possiamo ora calcolare lo stesso valore per il condensatore, la cui capacità è C=66.24pF=0.00006624µF (non dimentichiamo che se usiamo i MHz come frequenza, dobbiamo usare i µF per le capacità, non il pF!). Abbiamo quindi X=-1/2π·10.1MHz·0.00006624µF=-237.891Ω. I condensatori di questo tipo, a differenza delle induttanze, hanno ESR molto bassa per cui possiamo tranquillamente considerare R=0Ω:
ZC: 66.24pF@10.1MHz → RC=0Ω, XC=-237.891Ω
Il circuito accordato
Il nostro circuito accordato (antenna più accordatore) è composto da tre componenti: l’antenna, il condensatore e l’induttore. Siamo anche a conoscenza dell’impedenza R,X di tutti e tre i componenti.
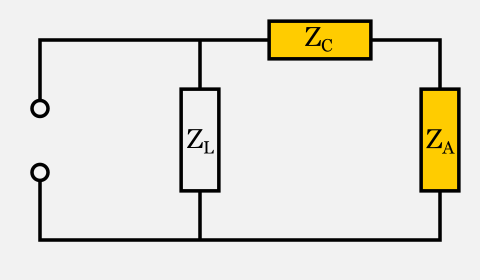
Questo è lo schema del circuito complessivo, dove ZA è il nostro carico (antenna), ZC è il condensatore e ZL è l’induttore:
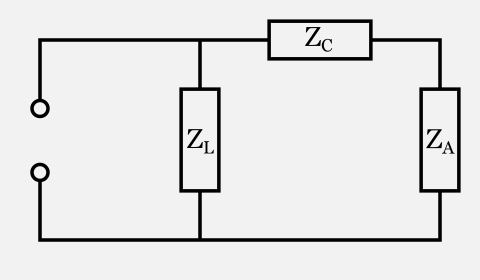
La prima cosa che notiamo è che ZC (il condensatore nell’accordatore) e ZA (l’antenna) sono in serie:
Se fossero stati semplici resistori in corrente continua, li avremmo sommati sostituendoli con un circuito equivalente costituito da un solo resistore.
Il fatto interessante è che anche le impedenze possono essere sommate e sostituite con un componente equivalente. L’operazione di “somma” tra impedenze deve prendere in ingresso la R e la X dei due addendi e ritornare come risultato una nuova coppia di R e X. In questo caso, il calcolo da eseguire per la combinazione in serie è piuttosto elementare perché basta sommare separatamente le R e le X:
RB = RC + RA = 0Ω + 29.65Ω = 29.65Ω
XB = XC + XA = -237.891Ω + 213.33Ω = -24.561Ω
A questo punto possiamo sostituire ZC e ZA in serie con una singola impedenza ZB definita come RB = 29.65Ω e XB = -24.561Ω ottenendo pertanto il seguente circuito equivalente:
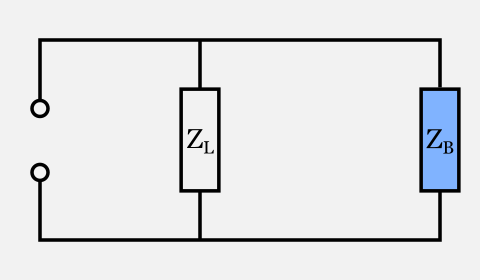
Ci sono ora rimasti due componenti in parallelo: qual’è la loro impedenza combinata?
La formula [2] per le resistenze in parallelo suggerisce che dovremmo calcolare il reciproco di ZL e di ZB, sommarli ottenendo ZD‘ e quindi calcolare il reciproco di ZD‘. Ma come si calcola il reciproco di un’impedenza che è formata da due numeri R e X?
L’impedenza R’, X’ reciproco di una data impedenza R, X si calcola con le formule qui riportate:
R’ = R/(R2+X2)
X’ = -X/(R2+X2)
Cominciamo quindi a calcolare il reciproco di ZL:
RL‘ = RL/(RL2+XL2) = 1/(12+59.5892) = 0.00028154
XL‘ = -XL/(RL2+XL2) = -59.589/(12+59.5892) = -0.0167769
Calcoliamo anche il reciproco di ZB:
RB‘ = RB/(RB2+XB2) = 29.65/(29.652+(-24.561)2) = 0.020002
XB‘ = -XB/(RB2+XB2) = -(-24.561)/(29.652+(-24.561)2) = 0.016569
Ora, secondo la formula [2], sommiamo i due valori in ZD‘ e ne calcoliamo il reciproco ZD:

Cominciamo calcolando ZD‘:
RD‘ = RL‘ + RB‘ = 0.00028154 + 0.020002 = 0.02028354
XD‘ = XL‘ + XB‘ = -0.0167769 + 0.016569 = -0.0002079
Ora calcoliamo il reciproco di ZD‘ per ottenere ZD e la “magia” sarà completa:
RD = RD‘/(RD‘2+XD‘2) = 0.02028354/(0.020283542+(-0.0002079)2) = 49.2959
XD = -XD‘/(RD‘2+XD‘2) = 0.0002079/(0.020283542+(-0.0002079)2) = 0.5053
L’impedenza finale dell’intero circuito è R=49.2959Ω X=0.5053Ω, cioè quasi un match perfetto (ROS=1.02) per l’impedenza desiderata di R=50Ω X=0Ω e corrispondente all’impedenza R=49.8Ω, X=0.05Ω misurata inizialmente dopo l’accordo.
Grazie ai componenti aggiunti dall’accordatore, l’intero circuito comprendente il carico è ora perfettamente accordato!
Potenza dissipata dall’accordatore
Quant’è la potenza realmente “persa” nell’accordatore? La potenza può essere dissipata solo dalla componente resistiva dell’impedenza. Se potessimo costruire accordatori con componenti ideali, cioè puramente reattivi, la potenza dissipata dall’accordatore sarebbe nulla e tutta la potenza andrebbe in antenna.
La potenza dissipata da ciascun componente può essere calcolata con regole analoghe a quelle utilizzate in corrente continua delle reti resistive. Non ci addentreremo in tali calcoli in questa sede, ma possiamo tenere presente che i nostri accordatori hanno resistenze interne molto basse e nella maggior parte di accordi, dissipano quantità irrilevanti di energia.
Questo fatto è evidente nell’immagine termica del mio accordatore di esempio che, nonostante stia alimentando un carico con ROS pari quasi a 33, è completamente freddo.

Conclusioni
Un accordatore è in grado di trasformare l’impedenza di un carico nell’impedenza richiesta dal generatore creando un circuito che, combinato in serie/parallelo con il carico, produce l’impedenza desiderata. Dato che i componenti aggiunti dall’accordatore sono di tipo reattivo, essi non dissipano potenza. Negli accordatori reali, dato che i componenti reattivi non sono ideali, una porzione in genere irrilevante di potenza è dissipata dagli stessi, mentre la quasi totalità dell’energia raggiunge il carico.


Grande Davide, sempre chiaro e “scientifico”
Perfetto. Grazie.
Yes IZ2UUF sempre chiaro e super, per fortuna ci sei.
Ciao IZ2UUF, conoscevo questi concetti attraverso le publicazioni di colleghi stranieri. Io sono un utilizzatore di questi accordatori CL LC oggi telecomandati si perché abitando in condominio e non avrei avuto la possibilità di installare tanti fili chiaramente uso la scaletta è un accordatore bilanciato fatto in casa no trasformatori 4:1 ecc. In sintesi ai fatto degli ottimi articoli ti faccio i miei personali complimenti vai avanti così.
Purtroppo in giro c’è tanta gente che non comprende un fico secco, denigra il prossimo e non approfondisce ma promuove idee e concetti totalmente errati.
Un cordiale e sincero saluto, Alfio IW9BID
Scusa, tutto quello che scrivi mi pare giusto, ma manca una considerazione ulteriore. Una volta che il circuito accordatore+antenna è accordato sicuramente il trasferimento di energia dal TX al circuito suddetto é massima. E non c’è disipazione sotto forma di calore essendo l’impedenza solo resistiva. Ma cosa possiamo dire dell’energia che si accumula ad ogni semionda nel campo magnetico dell’induttanza e in quello elettrico della capacità? Non è potenza sottratta al TX e persa ai fini della trasmissione (anche se non dissipata in calore) in quanto non raggiunge l’antenna? Saluti e grazie
Ciao Leonardo.
Se vuoi stabilire la solidità della tua teoria che l’energia accumulata nell’induttanza e nella capacità sia permanentemente sottratta alla trasmissione e non solo dilazionata, devi spiegare il bilancio energetico in maniera convincente.
Se tale energia non diventa calore e non diventa RF irradiata, dove va a finire? Si accumula all’infinito nell’induttanza come fosse una batteria che possiamo caricare all’infinito? O sparisce nel nulla violando il principio di conservazione dell’energia?
Spiega.
Ciao
Davide IZ2UUF
Complimenti !!!
Tutto chiaro e cristallino !!!
Ciao Davide,
ti ringrazio di cuore per questo articolo e per tutti gli altri che ho trovato su RKE per l’alto contenuto professionale e per la cura con cui li hai scritti.
A proposito di accordatori ho letto l’articolo “L’accordatore cambia il ROS dell’antenna …” su RKE 7/8 2020.
Provando a cercare informazioni sull’argomento (per me assillante/ossessionante in questo periodo) su “ARRL Antenna Book 25th ed.”, quello che ho trovato fin’ora è molto povero e superficiale “l’accordatore non sintonizza per nulla l’antenna, anche se collegato al punto di alimentazione dell’antenna. L’accordatore trasforma solo l’impedenza al connettore di uscita in una differente impendenza al suo connettore di ingresso” (paragrafo 24.1 pag. 3) (magari tu mi puoi indicare dove ne parlano in maniera più approfondita).
Queste poche righe (a me) fanno pensare che venga solo corretta l’impedenza non adatta del carico in una adatta per il nostro trasmettitore e che quindi tutta la potenza del tx possa essere inviata all’accordatore ma la potenza che in realtà arriva all’antenna sia quella al netto del return loss (tralasciando le dissipazioni sul cavo e sull’accordatore).
Dove finisce all’ora la potenza non irradiata? Ovviamente non può sparire per magia e io non ho ancora trovato una risposta in merito.
Il mio tarlo è che l’energia che non viene irradiata possa essere NON ACCUMULATA MA SCAMBIATA ad ogni ciclo dell’onda con il condensatore e la bobina dell’accordatore.
Nella prova descritta nell’art. su RKE sopracitato hai utilizzato un carico disadattato puramente resistivo e forse si potrebbe ripetere con uno che abbia anche una componente reattiva, in modo da avvicinarci di più ad una situazione reale. Credo che quella prova abbia messo un punto sulla questione, almeno per i carichi completamente resistivi e se si potesse replicare anche per quelli con una componente reattiva credo che potrebbe mettere fine alla questione.
Spero sia chiaro che non voglio affermare qualcosa di diverso alla tua teoria che è sostenuta da precise misurazioni. Piuttosto sto cercando il tuo aiuto per smontare definitivamente la mia.
Grazie ancora per il tuo prezioso contributo.
Con sincera ammirazione.
73 Andrea – IU3PDF
p.s.
Mi potresti inviare la lista di tutti gli articoli che hai scritto su RKE?
Ciao Andrea.
Considera un sistema formato da accordatore, cavo e antenna. Supponiamo che il tuo trasmettitore immette 100W nel sistema, cioè 100 joule ogni secondo. Questa energia può o accumularsi nel sistema o uscire dal sistema da qualche parte. Stabilito ragionevolmente che non possa accumulare energia all’infinito, altrimenti avremmo inventato la batteria del secolo, rimane solo la possibilità che l’energia che entra nel sistema, vi esca in qualche forma.
Le due forme più comuni sono calore e campo elettromagnetico.
Supponiamo che tu sostenga che la “potenza riflessa” non sia irradiata come campo E/M ma sia dissipata come calore secondo la tabella del mismatch loss: ROS=6, 50% di potenza riflessa, cioè 50W persi.
Detto questo, risulterebbe poco credibile affermare che sia con un accordatore di prima qualità e pochi metri di cellflex o un rottame cinese e un chilometro di RG174, la potenza dissipata sia sempre 50W. Verrebbe da dire che vengano dissipati 50W oltre alla potenza dissipata in calore naturalmente dai componenti dell’accordatore e del coassiale, cioè che 50W persi con ROS 6 sia un caso ideale che può solo essere peggiorato.
Ebbene, ipotizziamo un accordatore e una linea di trasmissione ideali, cioè privi di componente resistiva e quindi a perdita nulla, e mettiamoli nel sistema. Dovresti avere una perdita in calore di 50W esatti perché i componenti sono ideali e non aggiungono alcuna penalizzazione.
Ma qui sorge il problema? Chi dissipa i 50W in calore? L’accordatore e il cavo no, perché li abbiamo scelti ideali con resistenza nulla, per cui sono incapaci di dissipare energia in calore. E non c’è nessun altro componente.
L’unica opzione che rimane, che è quella vera, è che qualunque sia il ROS, a meno dell’energia dissipata da accordatore e linea in base alla loro qualità, la potenza viene tutta irradiata. Il fatto che la “potenxa riflessa” sia potenza persa, è un mito molto comune tra radioamatori e CB.
https://www.iz2uuf.net/wp/index.php/2017/07/30/il-mito-della-potenza-riflessa/
Ciao
Davide
Ciao Davide,
mi sono inventato questo test per capire se l’accordatore “inganna” la radio oppure no.
A-Strumento usato per la misurazione dell’antenna: nanoVNA V2 Plus4
B-Strumento usato per la trasmissione: Generatore di forme d’onda Juntek PSG9080
C-Strumento usato per misurare il segnale generato di 0dBm: Rigol DSA705
D-Strumento usato per misurare il segnale irradiato: Expert Electronics SunSDR2pro collegato ad un coassiale di circa 1mt (non terminato) che funge da antenna
E-Accordatore: PALSTAR AT1500CV (con circuito di tipo a T)
Test accordatore:
1 – Con “A” trovo la frequenza nella quale misuro -6dB R.L.: 29.000 MHz 22.8+j28.1 Ohm
2 – Accordo l’impedenza @29.000 MhZ con “E” misurando l’ingresso con “A”: 50.2-j0.1 Ohm (volore 11 su Input, 173 su Output e 375 sull’induttore)
3 – Con “B” applico il segnale alla frequenza di 29.000 MHz su “C” e regolo la tensione fino a misurare 0dBm
4 – Con “B” applico il segnale impostato al punto 3, senza passare per l’accordatore, e misuro con “D” il valore del segnale ricevuto: -82.3 dBm
5 – Con “B” applico il segnale impostato al punto 3, ma questa volta usando l’accordatore (impostato al punto 1), e misuro il valore del segnale ricevuto: -77.5 dBm
Deduzioni:
La differenza calcolata tra i due segnali misurati (-77.5 dBm) e (-82.3 dBm) è di +4.8 dBm, questo è il “guadagno” (o per meglio dire, la mancata perdita) per aver utilizzato l’accordatore. Anzichè “guadagnare” tutti i 6 dB , ne ha guadagnati 4.8 dB, mentre gli altri 1.2 dB sono stati persi come I.L. suppongo.
Questo da ragione a quello che sostieni tu, in quanto non è che il trasmettitore venga “ingannato” dall’accordatore facendogli credere di far arrivare all’inizio della linea di trasmissione tutta la potenza impostata quando in realtà ci sono 6 dB in meno, ma che invece l’accordatore non “inganna” propio nessuno in quanto riduce le perdite da 6 dB a soli 1.2 dB.
Per quelli poco abituati ad usare i dB, si può anche dire che se in trasmissione usiamo 100W/50dBm, con tutti e 6 i dB di perdita, arriverebbero all’inizio della linea di trasmissione solamente 39.8W/44dBm, mentre perdendone solo 1.2 dB, all’inizio della linea di trasmissione ne arriveranno ben 75.8W/48.8dBm (la potenza usata nelle prove di 0dBm è pari a 1 millesimo di Watt).
In altre parole ancora, considerando che alcuni rtx sono tarati fuori standard a 3 dBm per ogni punto di segnale (quando lo standard sarebbe di 6 dBm per ogni punto), si può dire che al posto di perdere due punti di smeter nella stazione che ci riceve, usando l’accordatore ne perdiamo solo meno di mezzo.
Gradirei molto un tuo parere sul test e sulle deduzioni.
Grazie.
Saluti
73 Andrea – IU3PDF
p.s.
Anche se la potenza era alquanto ridotta, durante le prove mi sono accertato che la frequenza di 29.000 Mhz fosse libera e prima di trasmettere ho comunque inviato il mio call avvisando delle prove in atto.